|
|
|
|
|
| |
Het gebruik van spreadsheets |
Waarom spreadsheets?
Spreadsheets zijn computerprogramma's die handig zijn bij het uitvoeren van berekeningen. Ten minste als dezelfde berekening meermalen moet worden uitgevoerd, want anders gaat het met een rekenmachine veel sneller. Alleen als je steeds dezelfde stappen in een berekening moet uitvoeren, kun je jezelf tijd besparen door de diverse steeds wisselende gegevens en de afzonderlijke stappen van een berekening in een rekenblad vast te leggen. Een rekenblad is een concrete toepassing van het spreadsheetprogramma en kan bewaard blijven voor toekomstig gebruik.
Bedrijven gebruiken veelvuldig spreadsheetprogramma's. Zij moeten vaak dezelfde berekeningen herhalen met andere getallen. Of zij moeten een afweging maken en een serie mogelijke oplossingen met elkaar vergelijken. Daarom is het nuttig het gebruik van spreadsheets te oefenen, ook als je een berekening maar één of twee keer hoeft uit te voeren.
|
Spreadsheets dwingen je na te denken over het PAD
Er is nog een andere reden die meer te maken heeft met het thema van deze website. Op school bieden rekenbladen de mogelijkheid om de voorbeelden beter te bestuderen en te kijken welke relaties tussen de diverse grootheden van belang zijn. Bedrijfseconomie lijkt een rekenvak, maar eigenlijk gaat het erom de juiste verbanden op te zoeken tussen de beschikbare gegevens en de onbekende grootheden. Bij toepassing van een spreadsheet komt naar voren dat de computer het rekenwerk doet, als het rekenblad maar duidelijk aangeeft welke relatie er tussen de vele grootheden bestaan.
Een ideaal leermiddel om spreadheets toe te passen, is de business game. In een game voor je een reeks cycli van planning & control uit, waarbij je als ondernemer steeds informatie krijgt over de resultaten die je in de voorafgaande cyclus behaald hebt. Met je spreadsheet kun je vooraf allerlei varianten doorrekenen om de meest gunstige te kiezen en achteraf kun je standaard uitrekenen hoeveel winst je gemaakt hebt, na aftrek van al je kosten.
Keuze van een spreadsheet-programma
Er zijn veel verschillende spreadsheetprogramma's op de markt. Elk programma heeft zijn eigen voor- en nadelen. Elk heeft ook zijn eigen bedieningshandleiding. Het is niet mogelijk om die hier te bespreken. Daarom is het goed te constateren dat de programma's ook veel gemeen hebben met elkaar en dat binnen de bedrijfseconomie meestal alleen eenvoudige toepassingen gevraagd worden.
Spreadsheetprogramma's zijn opgebouwd uit rekenbladen die bestaan uit kolommen en regels. Samen vormen zij een matrix van cellen. Elke cel is te typeren door een code die uit twee componenten bestaat: een verwijzing naar de kolom en een verwijzing naar de regel. Samen geven ze voor elke cel een unieke combinatie. De meeste spreadsheets hanteren hoofdletters om de kolommen en cijfers om de regels te karakteriseren. De aanduiding B4 verwijst dus naar een cel die in kolom B staat op regel 4. Het is handig om een apart blok gegevens te maken en een blok waarin uitsluitend berekeningen staan. Daarmee voorkom je dat je formules wist als je nieuwe getallen invoert. |
Voorbeeld van een spreadsheet
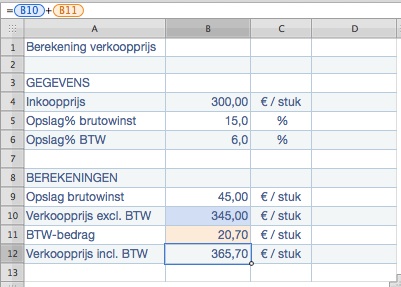
Formules: B9= B5/100 * B4 B10= B4 + B9 B11= B6/100 * B10 B12= B10 + B11
|
Grootheden hebben drie kolommen nodig
De celaanduidingen zijn belangrijk, omdat berekeningen vorm krijgen door verbindingen te leggen tussen cellen en daarmee tussen grootheden. Maar zoals je weet bestaan grootheden in principe uit vier delen: een economische notie, een naam, een waarde en een dimensie (of eenheid). De economische notie is de betekenis die een grootheid heeft. Die komt niet in het overzicht te staan, omdat je die moet herkennen aan de hand van de naam.
De andere drie delen komen in drie verschillende kolommen te staan! Dus als de naam van een grootheid in kolom A staat op regel 4, dan komt in kolom B op regel 4 de waarde van de grootheid te staan. Als die grootheid een eenheid heeft, dan komt die in principe in kolom C op regel 4. Vervolgens verbind je de cel in kolom B4 met een andere waarde om hem in een berekening in te bouwen.
De meeste grootheden hebben een dimensie, d.w.z. een aanduiding voor de betekenis van het getal dat bij de grootheid hoort. De inkoopprijs van de goederen wordt doorgaans uitgedrukt in euro per eenheid product. Gebruikelijk is om het euroteken voor het getal te noteren. Dat kan eventueel door een extra kolom te nemen in het rekenblad. In de meeste spreadsheets kun je echter ook voor kiezen om een geldeenheid automatisch voor het getal te plaatsen, zonder dat daarmee de mogelijkheid om met dat getal te rekenen, wordt ingeperkt.
Toepassing van een spreadsheet
Het is aanbevelenswaardig om een rekenblad steeds in vaste blokken in te delen. Het eerste blok is het gegevensblok dat in bovenstaand voorbeeld vier regels en vier kolommen omvat: twee kolommen voor de naam van een grootheid, één kolom voor de waarde en één kolom voor de dimensie-aanduiding. Door alle gegevens bij elkaar te zetten blijft het rekenblad overzichtelijk en is duidelijk welke grootheden de berekening aansturen.
De berekeningen zelf, met de namen van de tussenresultaten en het eindresultaat staan bijeen in een blok berekeningen. Als het rekenblad in gebruik is voor meerdere berekeningen tegelijk, kunnen meer berekeningenblokken afgebakend worden. Als de berekeningen complex zijn, is het ook mogelijk om extra tussenstappen toe te voegen. Bijvoorbeeld om de gegevens te bewerken. Dit kan de overzichtelijkheid ten goede komen. Zo kan het opslagpercentage brutowinst in het voorbeeld uitgedrukt worden als perunage (E5: +C5/100).
Tot slot is het mogelijk om de resultaten samen te brengen in een blok resultaten-overzicht. Bij een kleine opgave als in dit voorbeeld heeft dat geen nut, maar in complexere rekenbladen kan het erg nuttig zijn. Onderin de figuur staan de formules die in de diverse cellen ingevoerd moeten worden om de getallen te krijgen. Deze moeten als onderliggend model van het vraagstuk in het rekenblad worden opgenomen. Zodra één van de gegevens een ander getal krijgt, rekent het programma direct de nieuwe waarden uit die horen bij de andere grootheden. Het gaat er dus om de relaties tussen de grootheden goed vast te leggen. En kennis van die relaties behoort tot het economisch inzicht.
Bijzonderheden in het gebruik
Afkortingen zijn soms nodig voor de namen van de grootheden. Net als bij de dimensies zal de correcte naam soms te lang zijn om in beeld te brengen. De beperkte ruimte dwingen dan tot het maken van een keuze tussen een correcte naam vol afkortingen of een incorrecte, maar wel compacte naam. In plaats van 'verkoopprijs exclusief BTW' is in het voorbeeld gekozen voor 'verk.prijs ex BTW', maar even goed had er 'prijs excl. BTW' kunnen staan, of 'prijs ex'. De gebruiker kan zelf een strategie hiervoor ontwikkelen.
De breedte van de kolommen is op de meeste spreadsheets zelf in te stellen, en daarmee het aantal cijfers of letters dat binnen één kolom in beeld komt. Maar dat wil niet zeggen dat de niet-getoonde decimalen afwezig zijn. Je moet er rekening mee houden dat die decimalen bij berekeningen wel gebruikt worden. Daarom is het noodzakelijk delingen altijd te voorzien van een formule om het getal af te ronden op het aantal decimalen dat in beeld komt.
Tips voor onvoorziene omstandigheden
Er zijn allerlei kleine probleempjes die het gebruik van een spreadsheet-programma kunnen verstoren. Zo hanteren veel programma's de Amerikaanse notatie, waarbij de punt op de plaats staat waar in Nederland de komma gebruikelijk is en de komma op de plaats waar in Nederland een punt staat. Spaties zijn overigens ook tekens, net als letters en getallen. Meer verrassingen kunnen optreden, maar dat behoort allemaal tot de vaardigheid om computerprogramma's te hanteren.
Ook kunnen onverwacht foutmeldingen komen, bij voorbeeld als je begint met een minteken voor een berekening of een procent-teken voor een dimensievermelding. Het programma kan dit als het begin van een berekening interpreteren en om verdere instructies vragen. Een dergelijk probleem is op te lossen door eerst een spatie in te voeren.
|
|
|
|
|
|
|
|
| De bedoeling van Vakdidactiek Bedrijfseconomie
|
Vakdidactiek-bedrijfseconomie.nl is nauw verbonden aan de de websites bedrijfseconomische-begrippen.nl en bedrijfseconomische-modellen.nl. Zij biedt essenties van de vakdidactiek bedrijfseconomie aan in overzichtelijke eenheden, voor zowel leerlingen, studenten, als docenten.
Auteur is Fons Vernooij, die als eerste in Nederland is gepromoveerd op een onderwerp uit de vakdidactiek bedrijfseconomie (september 1993): “Het leren oplossen van bedrijfseconomische problemen. Didactisch onderzoek naar kostprijs- en nettowinstvraagstukken in het voortgezet onderwijs”. Deze dissertatie is de bron voor de pagina’s van deze site.
Mocht u tips of hints hebben dan ontvangen wij die graag via de webmaster Fons Vernooij.
|
|
|
| Website van Fons Vernooij: fons-vernooij.nl
|
Copyright © 1998 by Fons Vernooij en anderen.
Wij volgen het privacy-beleid van Google en zijn niet verantwoordelijk voor het selecteren van de advertenties in de Google vakken.
Registratienummer V.O.F. Adviesbureau CASA: KvK Rijnland: 58884114 / BTW 8532.22.848
Dossiernummer Stichting Onderwijsportaal: KvK Rijnland: 28092786 / BTW-nummer 8106.36.025
Webmaster: Fons Vernooij
Info over privacy en cookies: zie Privacybeleid
Leveringsvoorwaarden: zie bijgaand document
|
|
|
|
|